提案手法の実験結果を評価する指標として、再現率と精度、あとF値などがよく用いられます。他のWebページなどを参照すればすぐに分かる内容なのですが、自分自身のためのメモとして残しておきます。
まず、これらの指標が何かを示す前に、背景を少し説明しておきます。まず、あるデータベースから正解データをいかに正確にたくさん発見できるかという問題があり、それに対して提案手法はどの程度有用であるかを実験によって評価します。
ある手法では、与えられたデータセット全てを正解データであると認識したとします。この場合、確かにデータセットに含まれる正解セットの全てを発見したと言えるでしょう。しかし、それ以上に正解でないデータも正解としてしまっています。これでは、この手法は現実には役には立たないでしょう。
また、ある手法では、与えられたデータセットのほんの少しだけを正解データであると認識したとします。この場合、当たり外れはあるものの、当たれば正解と認識したデータ全てがその通りである可能性は高いと言えます。しかし、他にも存在するかもしれない正解データを認識することはできず、これもまた現実には役には立ちません。
ここで再現率(recall)とは、全ての正解データのうち、どれだけ正解であると認識したか示す割合です。上記の2つの手法をこれで比較すると、前者は再現率が限りなく1に近いのに対し、後者はほとんど0に近くなります。
また、精度(precision)*1とは、正解であると認識したデータのうち、本当に正解であるかを示す割合です。前者の手法では、精度はあまり良くない(0に近い)のに対して、後者の手法では1か0に近い値を示します。精度はよく適合率とも呼ばれます。
さらに、再現率と精度の調和平均(逆数の相加平均をさらに逆数にしたもの)を計算することで、F値(F-measure)を求めることができます。多くの場合、F値が高ければ有用な手法であると言えます。
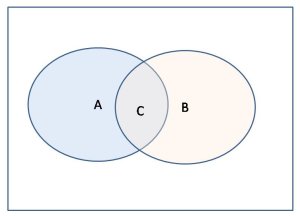
Aは正解と認識したデータ、Bは正解データ、Cは認識された正解データ。
再現率=C/B、精度=C/A
(2008/11/16 追記) ちなみに、上位n件精度のことを Precision at n とも言います。 これは、ある方法によって順序づけられたデータセットの上位n件にどれだけ正解データが含まれるかを示した指標です。
- *1:適合率とも言います。

コメントする